Does mandatory voting lead to more informed voting?

Rentschler, Lucas; Meyer, Jake

1 Introduction

Citizens often rely on the party affiliation of candidates when voting (Bonneau and Cann, 2015; Rahn, 1993; Schaffner and Streb, 2002). Indeed, Rahn states: “The most powerful cue provided by the political environment is the candidate’s membership in a particular political party…. The cue provided by the party label is simple, direct, and…consequential in shaping individuals’ perceptions and evaluations of political candidates.”

Yet there are many elections in which the ballots do not provide this basic information. These so-called nonpartisan elections often involve choosing city council members, county prosecutors, judges, natural resource managers, or sheriffs. By withholding partisan cues, the belief is that voters are more likely to acquire relevant information about candidates and make informed decisions.¹

However, Schaffner and Streb (2002) find that only a small proportion of voters in such elections are willing to express preferences and that many of these voters are “guessing.” In practice, voter participation in these elections is low relative to more high-profile races (Bowler, Donovan, and Happ, 1992; Feddersen and Pesendorfer, 1999; Ghirardato and Katz, 2006; Schaffner, Streb, and Wright, 2001). This is especially interesting since a voter’s probability of affecting electoral outcomes is significantly higher in most nonpartisan elections.

Low turnout and an uninformed electorate could (and perhaps do) lead to decreased government accountability and a weak connection between voter preferences and implemented policy. One potential solution, which has been adopted in many countries, is to enact mandatory voting laws.² Thus, understanding the effect of such laws is of practical importance.

Would mandating voter participation increase the number of voters who become informed about political issues? We address this question by developing a theory of information acquisition, which we then test in a laboratory experiment.

In our model we focus on whether voters will pay to acquire the information that is costlessly available in partisan elections: party affiliation.³ We establish that there is a symmetric perfect Bayesian equilibrium (PBE), regardless of whether voting is mandatory. In equilibrium, the model predicts that willingness to pay to learn candidate preferences is increasing in extremity of preferences, since more extreme citizens have more to lose if their preferred candidate loses.⁴

Interestingly, a mandatory voting law will increase informedness if information is cheap relative to the cost of voting. If the cost of information is high relative to the cost of voting, allowing for abstention increases informedness. The intuition behind this reversal is as follows. When abstention is permitted, the effective cost of information includes the cost of voting, since only informed voters would incur this cost. This lowers the level of informedness if voting is not mandatory. However, since uninformed citizens would not vote unless required to do so, the pool of expected votes is smaller relative to mandatory voting. This increases the probability of being the pivotal voter, effectively increasing the value of information. When the cost of being informed is low, the former effect dominates, while the latter effect dominates when the cost of information is sufficiently high.

Our laboratory experiments closely mirror our theoretical model. We vary the ability to abstain on a between-subject basis, and the cost of information on a within-subject basis. In a first series of experiments, we consider a low cost of information in which PBE predicts that mandatory voting will result in a more informed electorate, as well as a medium cost in which PBE predicts that allowing for abstention will result in a more informed electorate.

We find that information acquisition is higher under mandatory when the cost of information is low, in keeping with the PBE prediction. However, we also observe uninformed subjects voting when not required to do so. This, in effect, reduces the value of information when abstention is permitted, since the probability of being the pivotal voter is reduced. As such, we find that allowing abstention did not result in a significant difference in informedness for the medium cost.

To explain this behavior, we turn to agent quantal response equilibrium (AQRE).⁵ This model accounts for the systematic errors we observe at both the information acquisition and voting stages of the game. Most importantly, this alternative model is able to account for the uninformed votes we observe, and thus the finding that increasing the cost of information did not result in a more informed electorate with abstention.

We further noted that a prediction of the AQRE model is that if the cost of information were further increased, we would then observe a reversal in informedness. In response, we ran a second series of experiments, which are identical to the first series except that we replace the medium cost of information with a high cost. That is, we suggested an alternative model on the basis of our initial data and then tested the implications of this alternative model.

As the AQRE predicted, the high cost of information led to a higher level of informedness when abstention was permitted. While this certainly does not allow us to conclude that AQRE explains behavior, it is suggestive. We view our data as a single observation in the literature that considers QRE/AQRE models in voting games. We believe that the case for these models is compelling.

Our results have important implications for nonpartisan elections. Specifically, when learning about candidates’ policy platforms is sufficiently costly, mandatory voting laws can decrease voter informedness, since allowing for abstention increases the probability of being a pivotal voter, and thus the value of information. However, our experimental data suggest that this effect is substantially diluted since uninformed voters often opt to vote, despite it being irrational to do so. As such, in nonpartisan elections, mandatory voting is likely to lead to a more informed electorate unless the cost of becoming informed is quite high.⁶

Our results also have implications for the experimental literature on committee decision-making. In this literature, players are often assumed to have identical preferences and are incentivized to reach a group decision that matches some unobserved state of the world. Elbittar et al. (2020) and Großer and Seebauer (2016) study environments with endogenous information acquisition that allow abstention. Consistent with our data, they observe uninformed voting, which Großer and Seebauer (2016) call the “curse of the uninformed voter.” Significantly, they observe such over-voting when voting is costless, whereas we observe it in an environment where voting costs are strictly positive. Thus, our findings suggest that this is a relatively robust phenomenon, which would be a fruitful avenue for future research.

Previous research has found that the introduction of mandatory voting may increase turnout rates (Hoffman, Léon, and Lombardi, 2017), but it is less clear if it will lead to a more informed electorate. Other studies also find empirical evidence for a causal effect of citizen informedness on turnout decisions (Lassen, 2005; Feddersen and Pesendorfer, 1999; Strömberg, 2004), but evidence of causality in the other direction is scant.

Many studies have examined information acquisition in small group elections. A number of these studies show that uninformed citizens may prefer to abstain from voting. Others find that moderate citizens are less likely to become informed voters or to vote at all.

Feddersen and Pesendorfer (1999) model an election with costless voting and asymmetric information, finding that some of the less-informed voters always prefer to abstain. They also find that level increases in aggregate citizen informedness result in higher abstention rates for both the informed and uninformed. Battaglini, Morton, and Palfrey (2008) give experimental evidence that aggregate turnout will be positively correlated with the number of informed voters.⁷ In a theoretical environment, Oliveros (2013) shows that information acquisition and turnout decisions may in fact be uncorrelated for some voters.

Gersbach (1992) finds that the median voter is the least likely to purchase information in an election. Ortoleva and Snowberg (2015) show theoretically and empirically that moderate citizens have lower turnout rates compared to more ideologically extreme citizens. Matějka and Tabellini (2017) develop a theoretical model of voter information acquisition in a multi-dimensional policy election, finding that moderate voters invest less in information acquisition. They also point out that including party affiliation could lead to increased voter attention. Bhattacharya et al. (2017) study costly endogenous information acquisition in Condorcet settings as they vary group size and information precision. They find that subjects acquire information as predicted when information is precise, but with noisy information, subjects over-acquire information. They use quantal response equilibrium to rationalize this finding.

Other studies have compared voting laws with and without abstention, mostly with an eye to the welfare effects of mandatory voting. Börgers (2004) shows that in a costly voting environment with symmetric voter preferences and that allow for abstention, Pareto dominates mandatory voting in terms of welfare. Ghosal and Lockwood (2009) extend this work and find that mandatory voting may be welfare enhancing when facing uncertainty. Krasa and Polborn (2009) develop an alternative model that shows mandatory voting can be welfare enhancing when the support groups for candidates are sufficiently different. Krishna and Morgan (2012) study mandatory voting in a Condorcet setting and find that allowing for abstention is strictly welfare enhancing.

We are aware of only one study that examines the intersection of mandatory voting and endogenous information acquisition. Großer and Seebauer (2016) present a theory and an experiment to examine endogenous information acquisition in a Condorcet setting. In their theoretical and experimental study, voters have identical preferences and are able to acquire a costly signal about the state of the world before participating in a costless binary election. The researchers find that mandatory voting increases information acquisition relative to the case where abstention is permitted. They also observe marked levels of uninformed voting when abstention is allowed, contrary to equilibrium predictions.

2 Theory

There are $n\in \mathbb{N}$ risk-neutral voters participating in an election, where for simplicity we assume that $n$ is odd. Each voter has a type that is an $i.i.d.$ draw of a random variable with continuously differentiable density (distribution) $v(\cdot)$ $\left(V(\cdot)\right)$ on $[0,1]$ . Voter $i$ ‘s type is denoted as $v_i$ and is private information.

There are two candidates, $A$ and $B$ , who are running for office. Each candidate also has a type, which is private information. Candidate A’s (B’s) type is denoted $\gamma_A$ $\left(\gamma_B\right)$ and is independently drawn from a distribution with density $a(\cdot)$ $\left(b(\cdot)\right)$ with support on $\left[0,\frac{1}{2}\right]$ $\left(\left[\frac{1}{2},1\right]\right)$ . Voters are not initially able to distinguish which candidate is which but can each pay $c\geq0$ to do so.

Each voter first learns her type, and then all voters simultaneously decide whether or not to pay to learn candidate identities. After this information is observed by those who opted to pay $c$ , voters simultaneously make their voting decisions. Voting costs $\varepsilon\geq 0$ . The candidate with the most votes wins, with ties broken by fair randomization. The policy implemented, $\gamma$ , corresponds to the winning candidate’s type.

The payoff function for voter $v_i$ is

(1) $\begin{gather*} \pi_i(K,v_i,\gamma,e_i) = K -U\big(|v_i - \gamma|\big) - e_ic - w_i\varepsilon \end{gather*}$

where $K$ is a positive constant, and $-U\big(|v_i - \gamma|\big)$ is a continuous, twice differentiable, weakly concave function with a single peak at $v_i=\gamma$ . The indicator variable $e_i$ is equal to 1 if voter $v_i$ opts to learn candidate identities. We consider voting schemes with and without abstention, and the indicator variable $w_i$ is equal to 1 if the voter casts a vote.

In the interest of brevity, we add two assumptions. First, we restrict attention to environments in which $v$ is symmetric around $\frac{1}{2}$ . We also assume that $\big|\frac{1}{2}-E(\gamma_A)\big|=\big|E(\gamma_B)-\frac{1}{2}\big|$ . Each of these assumptions can be relaxed without substantively changing our results. Adding them allows us to focus on equilibria, which involve symmetric behavior of voters with types equidistant from $\frac{1}{2}$ .

2.1 Equilibrium

As is typical in the literature, we begin by assuming agents are sequentially rational and consider perfect Bayesian equilibria (PBE). In section 4.3, we examine the possibility that players noisily best respond to their beliefs in an agent quantal response equilibrium.

We first consider the voting stage of the game. When voting is mandatory, informed voters will vote for the candidate whose expected policy is closest to their type, while the uninformed voters will effectively randomize by arbitrarily selecting one of the two indistinguishable candidates. When abstention is permitted, a rational voter never prefers to vote when uninformed, as the candidates are indistinguishable, and voting costs $\varepsilon\geq0$ . Additionally, abstaining when informed cannot be part of an equilibrium, since knowing candidate identities does not have any value if a voter would not vote when informed. Thus, when abstention is permitted, only informed types vote.

The difference in equilibrium voting behavior across voting schemes introduces an important tradeoff, which underpins much of the following results. On the one hand, allowing abstention can increase the probability that a vote is decisive (since only effective cost of information from $c+\varepsilon$ to $c$ , since voters have no choice but to incur $\varepsilon$ . As we show below, this tradeoff leads to higher (lower) information acquisition under mandatory voting when $c$ is sufficiently low (high).

We now turn attention to the information acquisition decision, taking as given the equilibrium voting behavior described above. Notably, the value of learning candidate identities is higher for more extreme types, who will experience a higher loss than moderate types if the candidate on the opposing “side” wins the election. That is, the stakes of the election are higher for more extreme types, and thus the value of information is increasing in the extremity of type. In equilibrium, this leads to a cutpoint information acquisition strategy in which only voters with types weakly more extreme than the cutpoints become informed.⁸ Fixing the strategies of all other voters, voter $v_i$ will pay to acquire information if

(2) $\begin{gather*} E[\pi_i|v_i,e_i=1] - E[\pi_i|v_i,e_i=0] \geq 0. \end{gather*}$

Cutpoint types are defined by the pair of voter types who are perfectly indifferent to acquiring information, assuming that all other voters follow the cutpoint information acquisition strategy.

Under mandatory voting, if an interior cutpoint pair exists, the corresponding values of $v_i$ must satisfy the following equalities for $\delta\in\{1,-1\}$ :

(3) $\begin{gather*} \delta\cdot \frac{1}{2}\bigg(\int_{\frac{1}{2}}^{1} U\big(|v_i - x|\big)b(x) \hspace{3pt} dx - \int_{0}^{\frac{1}{2}} U\big(|v_i - x|\big)a(x) \hspace{3pt} dx\bigg) \binom{n-1}{\frac{n-1}{2}} \frac{1}{2}^{n-1} = c. \end{gather*}$

The left-hand side of equation (3), which we denote as $F(v_i)$ , is $v_i$ ‘s expected marginal benefit if her vote is pivotal (i.e., voter $v_i$ ‘s vote is a tie-breaker, resulting in her preferred candidate being elected), weighted by the probability that her vote is pivotal. Note that the probability of being pivotal is constant. As long as the cost of information is less than $\tilde{c}^m\equiv F(0)$ , there is a single voter type that satisfies this equation for each $\delta\in\{1,-1\}$ , which establishes the existence and uniqueness of this equilibrium under mandatory voting. All voters with types in the interior interval formed by the cutpoint pair will remain uninformed, while those with types more extreme will become informed.

Proposition 1. When voting is mandatory, there exists a unique symmetric PBE in which each voter $v_i$ follows a cutpoint information acquisition strategy in which

(4) $\begin{gather*} \begin{aligned} e_i = \begin{cases} 0 & \text{if } \hspace{5pt} v_i \in (v_l^m,v_r^m) \\ 1 & \text{if } \hspace{5pt} v_i \notin (v_l^m,v_r^m).\\ \end{cases} \end{aligned} \end{gather*}$

In this equilibrium, informed voters vote for their preferred candidate, and uninformed voters effectively randomize by arbitrarily selecting one of the two indistinguishable candidates.

Proof. See Appendix A.

A similar result follows when abstention is allowed. However, when voting is costly, uninformed voters will not vote in equilibrium. This means that the probability of being the pivotal voter will depend on the cutpoint types. We restrict attention to voter type distributions in which the probability of being pivotal is decreasing as the cutpoint types get closer to $\frac{1}{2}$ . Intuitively, this simply means that the probability of being the pivotal voter decreases as more voter types participate in the election.

If an interior cutpoint pair exists when abstention is possible, the two relevant types must satisfy the following equality for $\delta\in\{1,-1\}$ :

(5) $\begin{gather*} \begin{aligned} &\delta \cdot \frac{1}{2}\bigg(\int_{\frac{1}{2}}^{1} U\big(|v_i - x|\big)b(x) \hspace{3pt} dx -\int_{0}^{\frac{1}{2}} U\big(|v_i - x|\big)a(x) \hspace{3pt} dx\bigg) \times\\ &\sum_{t=0}^{\frac{n-1}{2}}\sum_{s=0}^{1} \binom{n-1}{2t+s}\binom{2t+s}{t+s} \big(1-2V(v_l^a) \big)^{n-1-s-2t}V(v_l^a)^{2t+s}&& = c + \varepsilon. \end{aligned} \end{gather*}$

We denote the left-hand side of equation (5) as $G(v_i,v_l^a)$ , which is again $v_i$ ‘s expected marginal benefit if her vote is pivotal, weighted by the probability of being the pivotal voter. For $c+\varepsilon \leq \tilde{c}^a\equiv \lim_{v_i\to 0^+} G(v_i,v_i)$ , there is a single voter type that satisfies this equation for each $\delta\in\{1,-1\}$ , which establishes the existence and uniqueness of this equilibrium when abstention is allowed. All voters with types in the interior interval formed by the cutpoint pair will remain uninformed, while those with types more extreme will become informed.

Proposition 2. When abstention is possible and $\varepsilon>0$ , there exists a unique symmetric PBE in which each voter $v_i$ follows a cutpoint strategy in which

(6) $\begin{gather*} \begin{aligned} e_i = \begin{cases} 0 & \text{if } \hspace{5pt} v_i \in (v_l^a,v_r^a) \\ 1 & \text{if } \hspace{5pt} v_i \notin (v_l^a,v_r^a).\\ \end{cases} \end{aligned} \end{gather*}$

In this equilibrium, informed voters vote for their preferred candidate, and uninformed voters do not vote.

Proof. See Appendix A.

When $\varepsilon=0$ , there is a continuum of equilibria, since uninformed voters are indifferent between voting or not. We focus attention on the unique limiting equilibrium as $\varepsilon \to 0^+$ , in which uninformed voters opt not to vote.

2.2 Comparing Voting Schemes

The cutpoint strategies described in Propositions 1 and 2 allow for equilibria where none, some, or all of the electorate will choose to become informed about candidate preferences, depending on the magnitudes of $c$ and $\varepsilon$ . If these parameters are such that at least some voters are willing to purchase information in either voting scheme, we can compare the equilibrium cutpoints to determine if allowing for abstention results in a more informed electorate.⁹ The costs of both voting and information acquisition will determine the relationship between the cutpoints in the two schemes.

Denote the maximum equilibrium willingness to pay for information for the most extreme voter types ( $v_i\in\{0,1\}$ ) when $\varepsilon=0$ as $\tilde{c}^m$ for mandatory voting, and $\tilde{c}^a$ when abstention is allowed. In both voting schemes, when $\varepsilon=0$ and $c\in[0,\tilde{c}^a]$ , a subset of the population will always choose to become informed when abstention is permitted. Thus, when abstention is possible, the expected number of voters who cast votes will be weakly less than the population total, increasing the probability of voter $i$ ‘s vote would be pivotal. For $c\in(0,\tilde{c}^a]$ the interval of uninformed voters under mandatory voting is a proper subset of the corresponding interval when abstention is permitted: $[v_l^m,v_r^m]\subset [v_l^a,v_r^a]$ . If $c>\tilde{c}^a$ or $c=0$ , then allowing for abstention has no effect on informedness: $[v_l^m,v_r^m] = [v_l^a,v_r^a]=[0,1]$ . Thus, mandatory voting will never result in a more informed electorate when the cost of voting is zero.

Lemma 1. When $\varepsilon=0$ , $[v_l^a,v_r^a]\subseteq [v_l^m,v_r^m] \hspace{2pt} \forall \hspace{2pt} c\geq 0$ .

Proof. See Appendix A.

When voting is sufficiently costly, many voters will abstain when permitted to do so, in order to avoid incurring $\varepsilon$ . In equilibrium, these voters also remain uninformed. Specifically, when $\varepsilon > \tilde{c}^a- \tilde{c}^m$ , allowing for abstention will never increase voter informedness. Even when the cost of information is small or zero, the relatively high cost of voting results in a smaller proportion becoming informed than if voting is mandatory.

Lemma 2. When $\varepsilon > \tilde{c}^a- \tilde{c}^m$, $[v_l^m,v_r^m]\subseteq [v_l^a,v_r^a] \hspace{2pt} \forall \hspace{2pt} c\geq 0$ .

In situations where $\varepsilon$ is positive but small, allowing for abstention may increase or decrease voter informedness relative to mandatory voting. When $c$ is low relative to $\varepsilon$ , allowing for abstention will decrease voter informedness because voters will prefer to avoid $\varepsilon$ , whereas $\varepsilon$ does not affect information acquisition choices under mandatory voting. However, when $c$ is large relative to $\varepsilon$ , the increased probability of being pivotal when abstention is possible will lead to increased informedness. As a result, whether or not abstention results in a more informed electorate depends on the value of $c$ when $\varepsilon$ is small.

Specifically, given $\varepsilon \in \big(0,\tilde{c}^a-\tilde{c}^m\big]$ , there exists a unique cost of information $\bar{c}$ , such that for $c=\bar{c}$ information acquisition will be the same under either mandatory or optional voting laws. For $c\in[0,\bar{c})$ , mandatory voting laws will result in a more informed electorate, and for $c\in (\bar{c},\tilde{c}^a-\varepsilon]$ , allowing for abstention will result in a more informed electorate. For $c>\tilde{c}^a-\varepsilon$ , no voters will become informed under either voting scheme.

Proposition 3.When $\varepsilon \in \big(0,\tilde{c}^a-\tilde{c}^m\big]$ , such that $[v_l^m,v_r^m]\subset [v_l^a,v_r^a]$ for $c\in \big[0,\bar{c}\big)$ , and $[v_l^a,v_r^a]\subseteq [v_l^m,v_r^m]$ for $c\geq \bar{c}$ .

Proof. See Appendix A.

2.3 Hypotheses

As Proposition 3 demonstrates, varying $c$ can lead to interesting differences in equilibrium behavior across voting schemes. These differences are the primary motivation for our experimental design. For concreteness, we explicitly list the predictions we are primarily interested in evaluating.

First, when the cost of voting is positive, uninformed types do not vote when abstention is permitted. Of course, under mandatory voting, uninformed types must always vote, although their votes are random.

These predictions regarding voting behavior have important consequences for information acquisition. In particular, because $\varepsilon$ is paid by all types when voting is mandatory, but is only paid by the informed types when abstention is permitted, the effective equilibrium cost of information is $c$ under mandatory voting, and $c+\varepsilon$ when abstention is permitted. When the cost of information is low ( $c<\bar{c}$ ), this results in more information acquisition under mandatory voting.¹⁰ However, as $c$ increases, so does the probability of being the pivotal voter when abstention is permitted. At $\bar{c}$ , these effects balance each other, so that equilibrium information acquisition is the same with or without abstention. For $c\in\big(\bar{c},\tilde{c}^a-\varepsilon\big]$ , the increased effective cost of information under abstention has a smaller effect on information acquisition than the increased probability of being a pivotal voter, and allowing for abstention increases voter informedness.¹¹

Thus, the second prediction of interest is that increasing $c$ can reverse the ranking of information acquisition across voting schemes: when $c<\bar{c}$ , information acquisition is higher under mandatory voting, and that, when $c>\bar{c}$ , allowing abstention increases information acquisition.

The third prediction of interest concerns the set of types that become informed. Since more extreme voter types have more to lose, their value of information is higher. In equilibrium, provided $c$ is not too high, this means that there is an interval of moderate types that remain uninformed, and that only the more extreme types outside this interval become informed.

3 Experimental Design

In each experimental session, 15 subjects participated in a voting game for 50 rounds. The subjects were randomly sorted into groups of 5, and these groups were randomly re-matched in each of the 50 rounds. Identities were anonymous within and across rounds.

In each round, each subject was assigned a type $v_i$ that was an \ $textit{i.i.d.}$ draw from a discrete uniform distribution on $\{1,2,...,100\}$ . Types were private information.

Each group was tasked with selecting either Option A or Option B via majority vote (ties were broken randomly). The per-subject cost of voting was 2. The selection of Option A (B) would result in a policy, $\gamma$ , that was an $\textit{i.i.d.}$ draw from a discrete uniform distribution on $\{1,2,...,50\}$ $\big(\{51,52,...,100\}\big)$ . The realized policy associated with each Option was not known to subjects when they voted. Further, the two Options were indistinguishable unless a subject paid $c>0$ .

Each subject’s payoff for the round was

(7) $\begin{gather*} \pi_i = 100 - |v_i - \gamma| - c e_i -2w_i \end{gather*}$

where $e_i$ is equal to one if a subject paid to get information, and $w_i$ is equal to one if a subject voted.

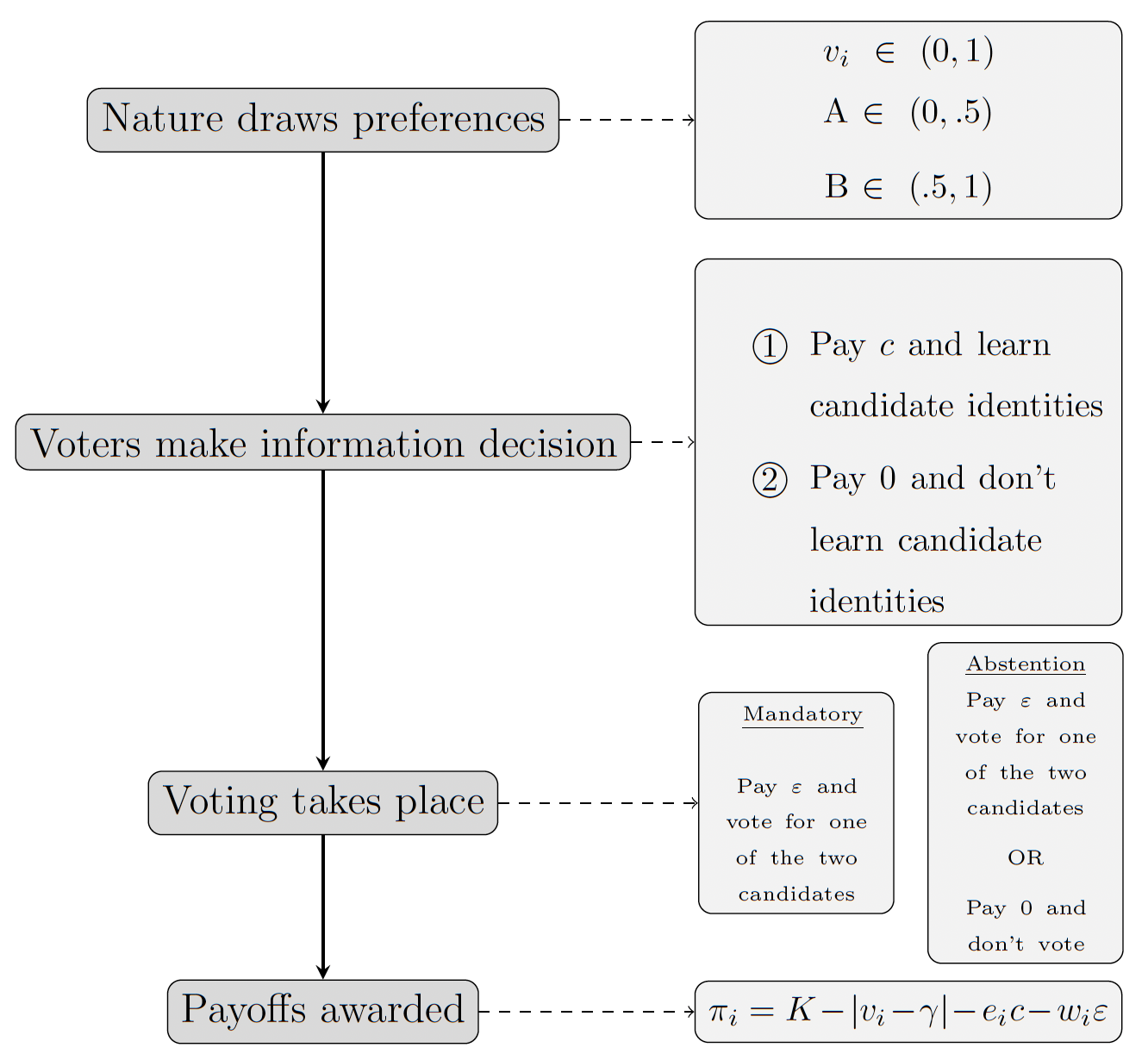
After learning their types, subjects simultaneously decided whether or not to pay to observe Option identities and then proceeded to the voting stage. If a subject chose not to pay, then the Options were both labeled as “Option ?” To ensure that Option identities could not be inferred, the order of the Options was randomized in each round, and this was common knowledge. If a subject paid to learn Option identities, then the corresponding labels were revealed during the voting stage. After votes were cast, all subjects observed which Option won the election, as well as the resulting $\gamma$ . Each subject also observed her own payoff for the round. The sequence of events in each round is displayed in Figure 1. At the end of the 50 rounds, 20 rounds were randomly chosen for payment.

We employed a $2\times3$ design. Whether abstention was permitted was varied on a between-subject basis. The cost of learning Option identities was either 3, 9, or 15, and was varied on a within-subject basis. We refer to these as the low, medium, and high-cost treatments. When abstention was permitted, we refer to treatments as AL, AM, and AH, when $c$ was low, medium, and high, respectively. Similarly, when voting was mandatory, we refer to treatments as ML, MM, and MH, when $c$ was low, medium, and high.

The cost of learning Option identities was constant within the first and second half of each session. In all sessions, subjects faced a cost of information $c=3$ in one half of the experiment, and $c=9$ or $c=15$ in the other. We varied the order of this within-subject variation to control for order effects, and this is perfectly balanced across the sessions.

We ran a total of 24 sessions. In 12 of these, abstention was permitted, with half varying $c$ between low and medium, and the others varying $c$ between low and high. Voting was mandatory in the remaining 12 sessions, and half varied $c$ between low and medium, with the other half varying $c$ between low and high.

In all sessions, subjects were seated at terminals with dividers and communication was not allowed. Physical copies of instructions were administered and read aloud by the experimenter.¹²After reading the instructions, the experimenter administered a quiz, and each subject was required to correctly answer every question before the session could advance.¹³ Sessions lasted about an hour. At the conclusion of a session, subjects were called individually to receive payment. All subjects received $\$5$ as a show-up fee, in addition to their in-game earnings. Earnings throughout the experiment were denominated in points, which were exchanged for dollars at a rate of one USD per 70 points. Average total earnings was $\$23.87$ , with a range of $[\$18.96, \$28.41]$ . Participants were recruited from the student population at Utah State University. No participant had any experience with any type of voting experiment. The experiment software was coded in z-Tree (Fischbacher, 2007).

In the spirit of Roth (1994), we wish to describe the process through which we arrived at our final experimental design. Initially, we relied on the PBE predictions and ran sessions 12 in which $c$ was varied between low and medium. The results from our initial sessions provided some support for the equilibrium predictions. However, subjects deviated from equilibrium predictions in interesting ways. First, information acquisition decisions did not follow a cutpoint strategy. While extreme types were much more likely pay to learn Option identities, they did not always do so, and moderate types frequently became informed. Second, when abstention was permitted, uninformed subjects often cast votes, despite this being costly. When considering treatment effects, we found that increasing $c$ decreased informedness, holding the voting scheme constant. Further, for $c=3$ , informedness was higher when voting was mandatory, as predicted. However, for $c=9$ , this finding did not reverse, contrary to equilibrium predictions.

In light of these observations, we hypothesized that an agent quantal response equilibrium (AQRE) was a better explanation for our data than the PBE predictions. An important implication of this model is that when abstention is permitted, uninformed voters will sometimes vote, reducing the probability of being a pivotal voter, and thus reducing the value of information. This then “dilutes” the effect of increasing $c$ . We fit an AQRE model to our initial data, and noted that for $c=9$ , the level of informedness was predicted to be slightly higher when voting was mandatory. This prediction is consistent with our data (and counter to the PBE predictions). We also noted that this model predicted that informedness would flip for higher levels of $c$ .

Rather than merely note that an alternative model was a better fit for our data, we decided to test this particular implication of our preferred model explicitly. To determine whether sessions with a higher $c$ would yield sufficient power, we performed a power analysis that accounted for the observed noisiness of behavior using an AQRE, following Woods (2023).¹⁴ This power analysis relied on predictions from an AQRE model with estimates of $\lambda$ obtained from our initial data. These predictions suggested that we would observe a more informed electorate with abstention when $c=15$ and that running an additional 12 sessions with $c$ varied between $c=3$ and $c=15$ would yield sufficient power to test this prediction.¹⁵

3.1 PBE Point Predictions

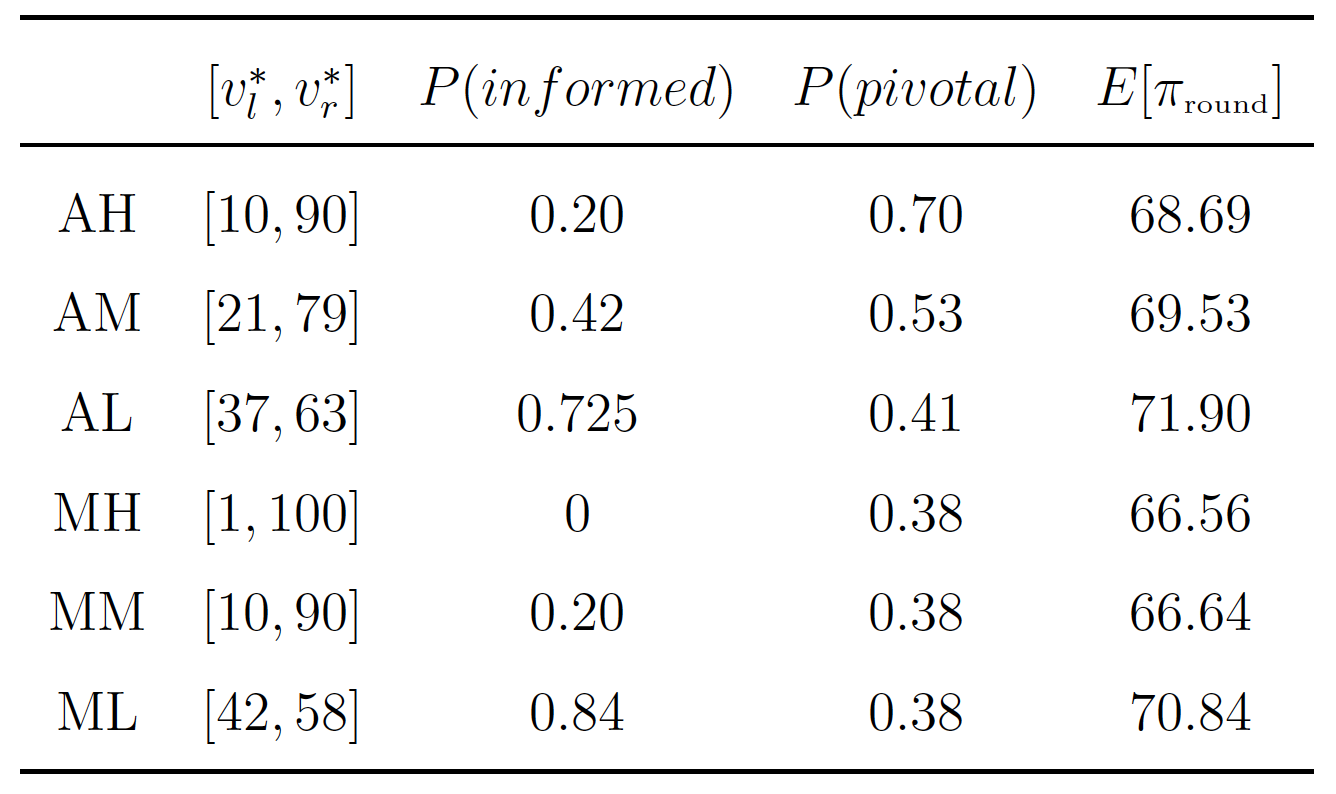
The PBE predictions for each of the six treatments are summarized in Table 1. In all treatments in which abstention is permitted, uninformed types are predicted not to vote. Behavior at the information acquisition stage is described by reporting the interior interval of types that are predicted not to become informed. Note that these intervals reflect that only extreme types are predicted to become informed, as they stand to lose more than moderate types when the “wrong” Option wins more votes. Further, note that for both voting schemes, the width of the interval of uninformed types is increasing in $c$ . Table 1 also reports, for each treatment, the probability that a vote will be pivotal, and the ex-ante expected payoff of a participant in a given round. Note that probability of being pivotal is increasing in $c$ when abstention is permitted, and is constant when voting is mandatory.

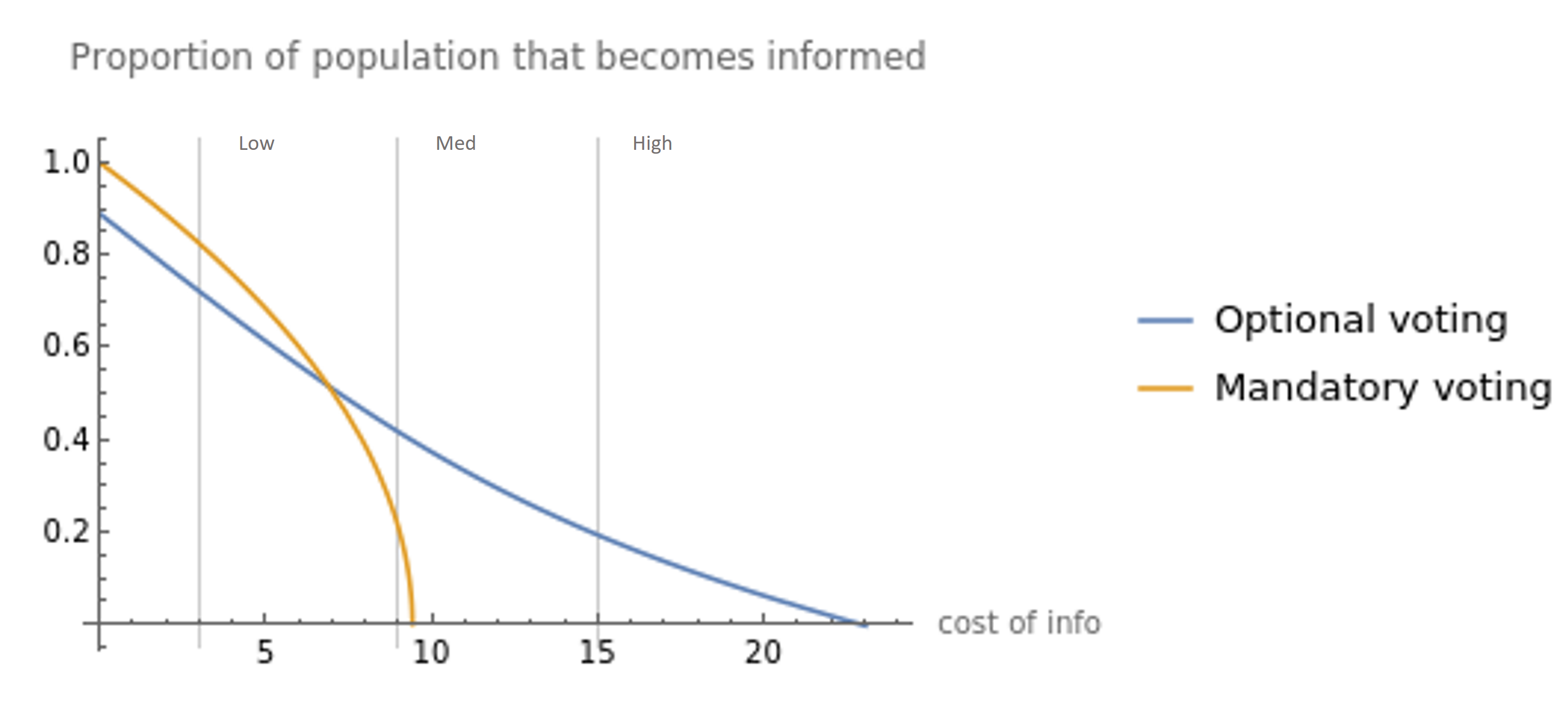
Figure 2 summarizes the equilibrium level of informedness across voting schemes as $c$ is varied. Importantly, when $c=3$ , mandatory voting is predicted to result in a strictly more informed electorate than when abstention is permitted. When $c=9$ , the cost of information is sufficiently high that this prediction reverses. Note that both voting schemes predict that some types will become informed when $c=9$ , although this set of types is larger when abstention is permitted. When $c=15$ , no types are predicted to become informed when voting is mandatory. However, when abstention is permitted, a relatively small set of extreme types are predicted to pay.

4 Results

In each session, subjects face one cost of information in the first half of the experiment, and another cost in the second half. We refer to the 25 rounds in which the cost of information was held constant within a session as a block. In all non-parametric tests, we take the average of all decisions within a block as an independent observation. Thus, when $c=3$ , we have 12 observations in each voting scheme. For $c\in\{9,15\}$ , we have 6 observations per voting scheme. Since $c$ is varied on a within-subject basis, one concern is that order effects may impede our ability to make inferences about the effect of changing $c$ within a given voting scheme. To account for this, we varied the order in which costs were presented: half the time a session started with $c=3$ , and half the time a session started with the relevant higher cost. Note that this variation in order is perfectly balanced. In addition, ex-post, we ran regressions to assess whether the order of the variation in $c$ affected behavior. We found no evidence that our results are driven by order effects. In what follows, we report $p$ -values from two-tailed tests. Unless otherwise noted, we employ the Wilcoxon signed-rank test for comparisons with matched pairs, and the Mann-Whitney U test for comparisons without matched pairs.

4.1 Information Acquisition

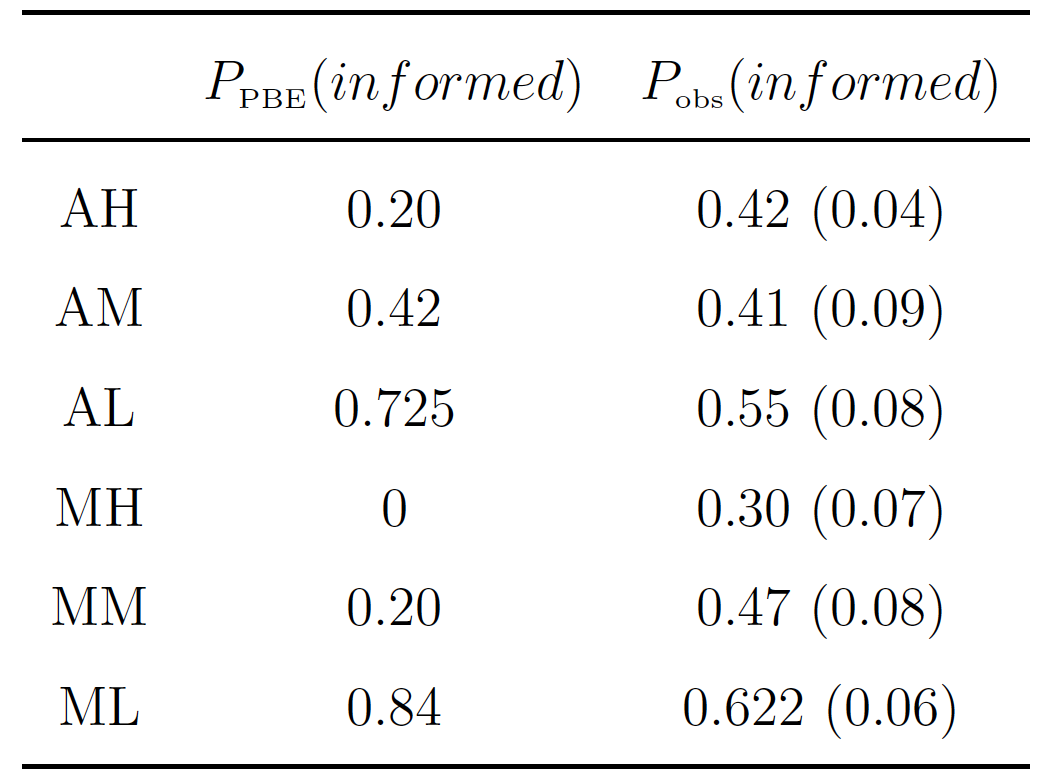
Our primary outcome of interest is the frequency with which voters pay to learn Option identities. Table 2 contains summary statistics of this outcome for all treatments, alongside the associated PBE predictions. The predictions reported correspond to the predicted behavior for the actual types realized during the experiment, as opposed to ex-ante expectations. Interestingly, behavior is less responsive to changes in the cost of information than PBE predicts. In particular, when $c=3$ , we see more information acquisition than predicted both when voting is mandatory ( $p=0.002$ ), and when it is optional ( $p=0.002$ ). However, when moving to $c=9$ , we see that informedness falls substantially less than predicted. In fact, we see more informedness than PBE predicts when voting is mandatory ( $p=0.028$ ) and are unable to reject the null that the level of informedness conforms to PBE predictions when abstention is permitted ( $p=0.917$ ). When further increasing the cost of information to $c=15$ , we find that informedness exceeds PBE predictions both when voting is mandatory ( $p=0.028$ ) and when abstention is allowed ( $p=0.028$ ).

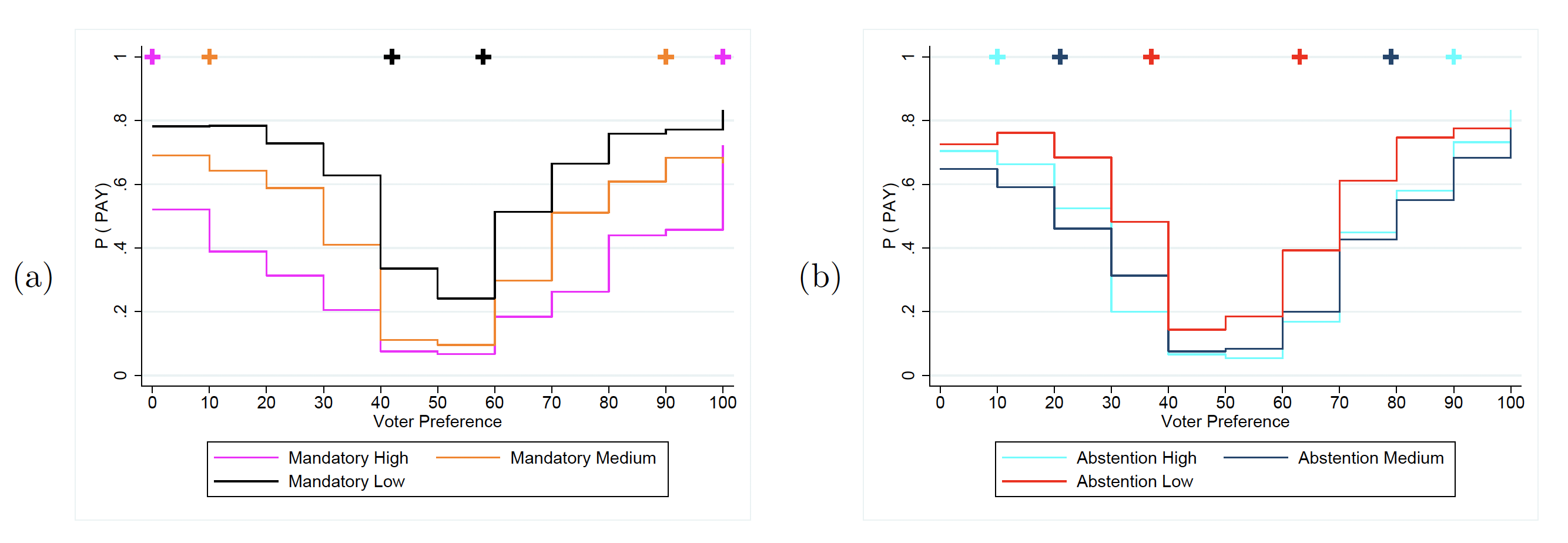
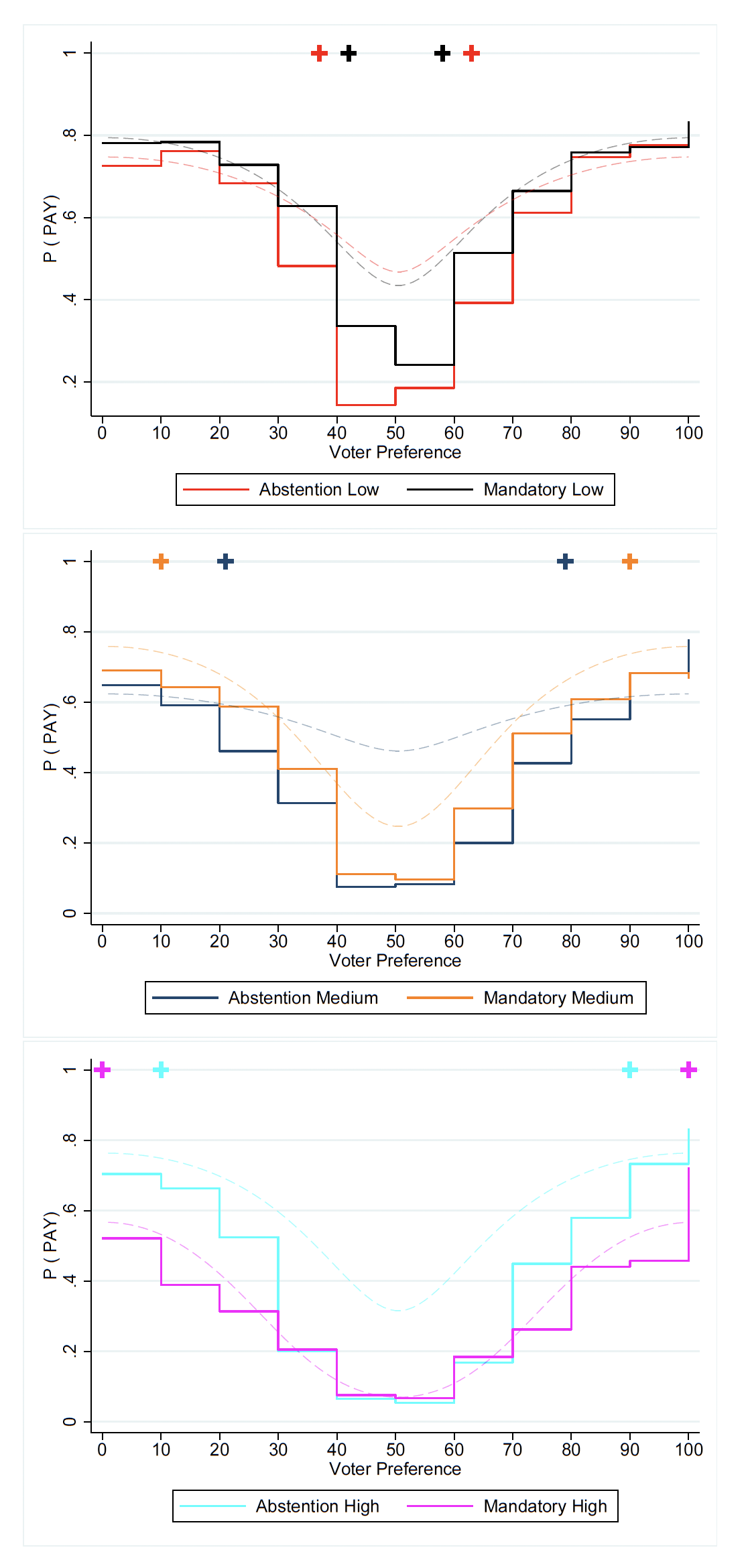
To better understand information acquisition decisions, we break them down by type. Figure 3 illustrates information acquisition choices by treatment, with types aggregated in bins of ten, as well as the relevant PBE predictions. Across all treatments, the qualitative prediction that more extreme types are more likely to become informed is borne out. However, as one might expect, subjects do not employ a cutpoint information acquisition strategy, and observed decisions are much noisier than predicted. In particular, moderate types are more informed than predicted while extreme types are less informed than predicted.

The implications of these deviations from PBE predictions are interesting. Most significantly, while mandatory voting leads to a higher level of informedness when $c=3$ ( $p=0.0243$ ), the predicted reversal of this finding when $c=9$ is not observed. When $c=9$ , average information acquisition remains higher under mandatory voting, though the difference is not significant ( $p=0.522$ ). However, when $c$ is further increased to $c=15$ , the predicted reversal emerges: informedness is higher when abstention is permitted ( $p=0.007$ ). As we will show below, these results can be explained by the irrational voting decisions of uninformed voters in the abstention treatments. Specifically, votes cast by uninformed types when abstention is possible reduces the probability of being the pivotal voter. Since the reason the value of information is increasing in $c$ under abstention is an increased probability of being pivotal, these irrational votes reduce the effects of higher $c$ .

Turning attention to the effects of changing the cost of information within a given voting scheme, we find that increases in $c$ lead to decreases in informativeness when voting is mandatory. This is true considering an increase from $c=3$ to $c=9$ ( $p=0.028$ ), as well as when considering an increase from $c=9$ to $c=15$ ( $p=0.004$ ). When abstention is permitted, we find a similar result when $c$ increases from $c=3$ to $c=9$ ( $p=0.028$ ). However, when increasing $c$ from $c=9$ to $c=15$ , average informedness actually increases by about 1 percentage point, and there is no significant difference ( $p=0.873$ ). That is, when abstention is possible, subjects do not meaningfully respond to an increase in the price of information from $c=9$ to $c=15$ . This is striking and is likely driven by the relatively high probability of being pivotal when $c$ is relatively high. To see this, recall that when voting is mandatory the probability of being the pivotal voter does not depend on $c$ and that we do see a drop in informedness when $c$ increases from $c=9$ to $c=15$ in the absence of abstention.¹⁶

4.2 Voting Behavior

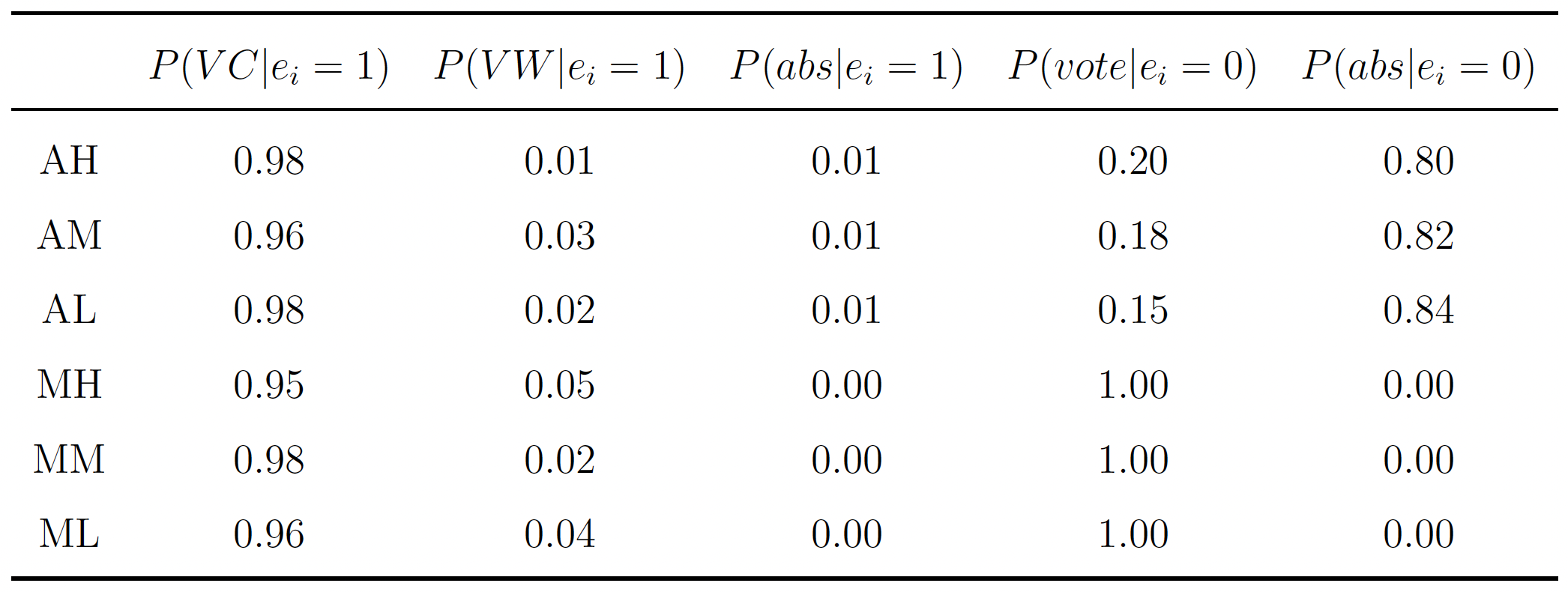
We next turn to voting decisions, since the choice to acquire information depends on beliefs regarding voting behavior. Table 3 contains summary statistics of voting behavior broken down by information acquisition choice. Recall that when abstention is permitted, PBE predicts that uninformed subjects will not vote, since doing so is costly and the two Options are indistinguishable. Further, since becoming informed is only worthwhile if a subject wishes to vote, informed subjects are always predicted to vote by PBE and to vote for the Option that, in expectation, is closest to their type.

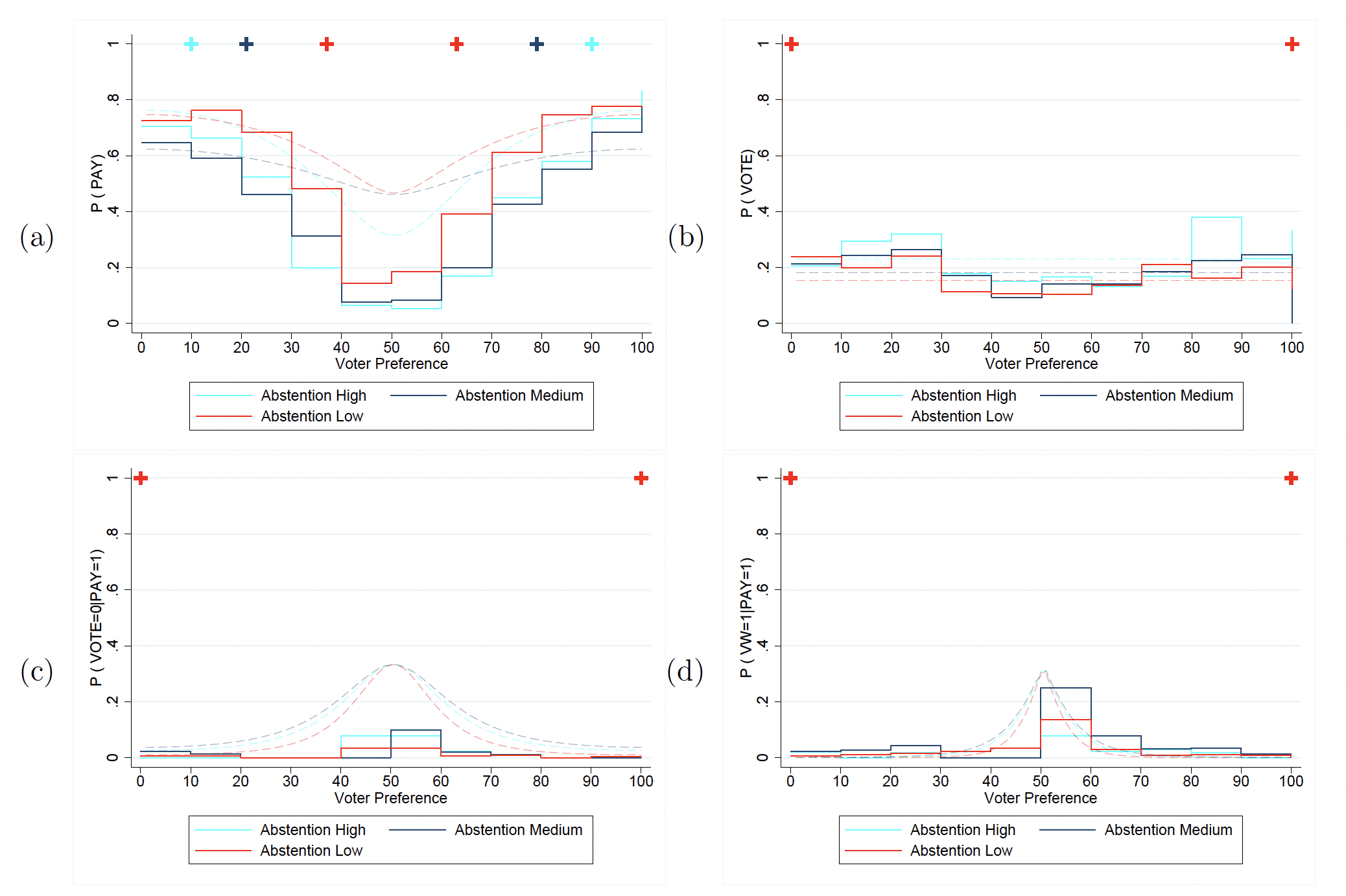
We observe relatively few instances in which informed voters vote for the Option that does not maximize their expected payoff (the “incorrect” Option). Similarly, informed voters seldom abstain from voting when permitted to do so. Interestingly, when abstention is possible, uninformed subjects vote fairly frequently: 15.1% of uninformed voters vote in AL, 17.6% in AM, and 20.0% in AH choose to vote.

Importantly, when uninformed subjects vote without being required to do so, the value of information under abstention is effectively diluted since uninformed votes reduce the probability of being the pivotal voter. Thus, a larger increase in $c$ would be required to reverse the ranking of informedness by voting scheme. As discussed, this is consistent with our data in the information acquisition stage of the game.

Such “over-voting” by uninformed subjects has been observed in previous experimental studies in similar environments. In particular, Elbittar et al. (2020) and Großer and Seebauer (2016) study voting games in which voter preferences are aligned, and players are incentivized to vote in accordance with an unobserved state of the world. Before voting, subjects can purchase information that is correlated with the unobserved state. In both studies, voting by the uninformed is observed. Elbittar et al. (2020) suggest that such “over-voting” is driven by biased perceptions of the induced common prior belief regarding the state of the world. However, this explanation cannot explain our data, since such priors are not present in the games we study. Großer and Seebauer (2016) offer several other possible explanations. In particular, they argue that such “over-voting” could be explained by subject confusion regarding the negative effect such votes could have on the likelihood that the votes match the state. They also argue that uninformed voting may be driven by a desire to avoid negative reciprocity in which not voting leads to a reduction in information acquisition by other group members in future rounds (since information acquisition by any player can improve outcomes for all in their environment). Finally, they suggest that uninformed votes could be driven by perceived normative expectations regarding the social desirability of voting, such that some people have an aversion to not voting.

Only the last of these explanations could potentially explain “over-voting” in our experiment. However, if an individual level aversion to abstention drove behavior, we would expect “over-voting” would be due to a subset of subjects who consistently vote when uniformed. On the contrary, we find considerable heterogeneity: of those subjects who ever had to decide whether to vote when uninformed, 42.7% opted to vote at some point in the experiment.

Unfortunately, our experimental design does not allow us to conclude the precise driver of this “over-voting.” However, the fact that such behavior is an apparently robust phenomenon across different environments makes it a promising avenue for future research. This is particularly true since there is no cost for casting a vote in both Elbittar et al. (2020) and Großer and Seebauer (2016), and we observe such voting when the cost of voting is strictly positive. Thus, we provide preliminary evidence that what Großer and Seebauer (2016) term “the curse of uninformed voting” is robust to a strictly positive cost of voting.

4.3 Agent Quantal Response Equilibrium

Our data differ substantially and systematically from the PBE predictions, which suggests that our data could be better explained by an alternative model. Such an alternative model should be able to account for three important features of our data. First, when abstention is possible, uninformed voters frequently vote, despite it being costly to do so. Second, more extreme types are more likely to become informed, but these information acquisition decisions are noisier than predicted by PBE. Third, when $c = 3$ , informedness is higher when voting is mandatory, but the effect of increasing $c$ on informedness is not as stark as predicted by PBE. In particular, an alternative model should account for the fact that the rate at which informedness declines in c is higher when voting is mandatory (so that for $c = 15$ allowing abstention results in more informedness). It should also account for the fact that these rates of decline are lower than predicted by PBE.

Quantal response equilibrium (QRE), which is frequently utilized to explain behavior in voting games, is just such an alternative model.¹⁷ QRE generalizes Nash equilibrium by allowing for systematic errors in decision-making such that the likelihood of a particular error decreases in its costliness (McKelvey and Palfrey, 1995). Since our model involves a sequence of decisions, the appropriate variant is agent quantal response equilibrium (AQRE), which imposes a stochastic version of sequential rationality (McKelvey and Palfrey, 1998). AQRE assumes that errors at one information set are independent of the errors at another information set. In particular, at each of a player’s information sets, it is assumed that a distinct “agent” noisily best responds to the player’s equilibrium beliefs, which account for errors on the part of other players and by her “agents” at other information sets.

For simplicity, and in line with the existing literature, we consider AQRE such that decisions are made using a logit response function in which a single parameter $\lambda$ determines the level of noise present in a decision. Specifically, we assume that when type $v_i$ must make a decision with possible actions $A\in\{a_1,a_2\ldots,a_m\}$ , the probability that action $a_j\in A$ is chosen is given by

$\begin{equation*} Prob(a_j) = \frac{e^{\lambda E(\pi_i|a_j)}}{\sum_{k=1}^{m}e^{\lambda E(\pi_i|a_k)}}, \end{equation*}$

where $E(\pi_i|a_k)$ denotes the profit of type $v_i$ conditional on choosing action $a_k$ . Note that if $\lambda=0$ , then all possible actions are equally likely, and as $\lambda \to \infty$ , the action which maximizes expected profit is chosen with certainty. To account for the fact that the complexity of choices, strategic or otherwise, differs within our extensive form game, we consider AQRE in which $\lambda$ varies across decision stages.¹⁸ In addition, we consider AQRE in which $\lambda$ is permitted to vary across treatments.

We estimate several AQRE models via maximum likelihood. Ex-ante, we committed to using the Bayesian information criterion (BIC) for model selection to ensure we are not overfitting our model. We consider a model with a single $\lambda$ for all treatments and decision stages, a model in which $\lambda$ varies only by voting scheme, a model in which $\lambda$ varies by decision stage and voting scheme, and a model in which $\lambda$ varies by treatment and decision stage. Note that we do not consider cases in which $\lambda$ varies by type, as this would result in an extremely large number of free parameters.

We follow the maximum likelihood procedure described in Großer and Palfrey.¹⁹ The procedure is complicated because for a given vector of $\lambda$ ‘s, we must solve for the corresponding AQRE to evaluate the likelihood function.²⁰ Thus, we perform a grid search, in which we finely discretize the set of possible $\lambda$ ‘s, calculate the associated AQRE for each of these possibilities, and then evaluate the likelihood function for each of these possibilities to select the optimal value(s) for $\lambda$ . Of the models, BIC is minimized when we allow $\lambda$ to vary both by treatment and by decision stage. In the interest of brevity, we relegate further details of both computing the AQRE predictions and the maximum likelihood procedure for selecting parameters to Appendix D. Below, we discuss the AQRE predictions for both the information acquisition decision and the voting decision.

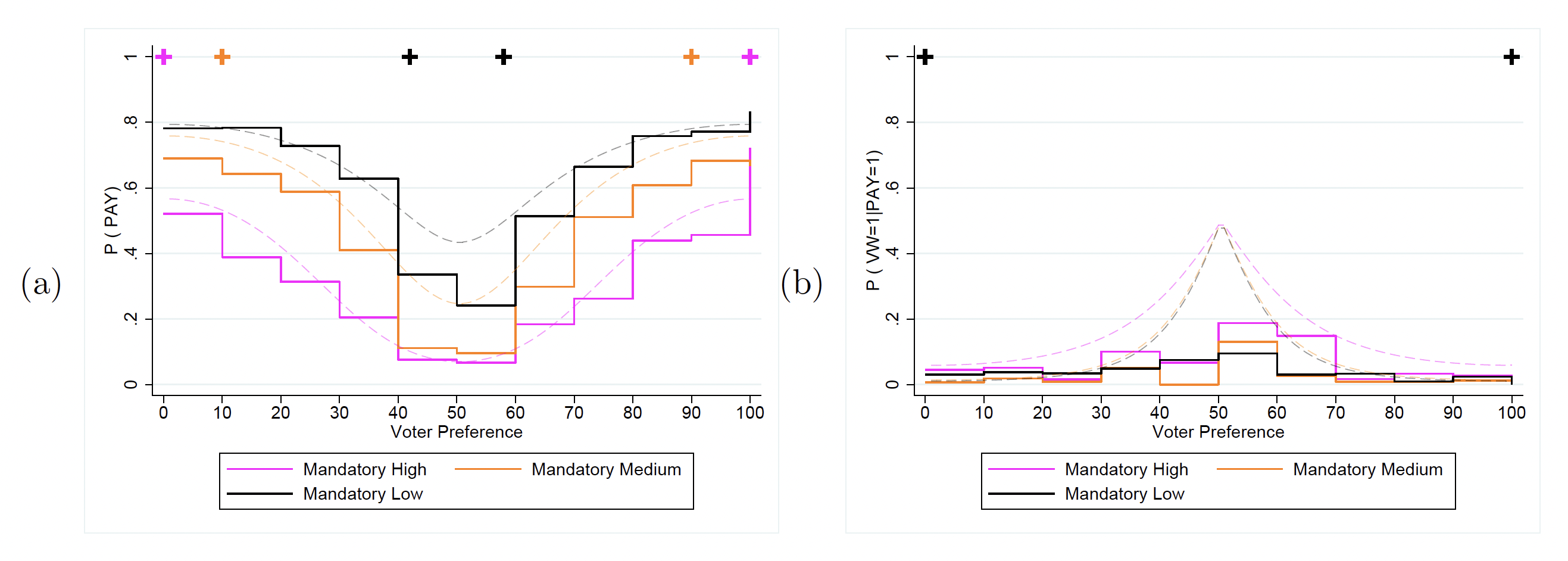
We first consider the effect of increasing the cost of information, holding the voting scheme constant. Figure 4 illustrates the observed decisions at each stage of the game when voting is mandatory, as well as the corresponding PBE and AQRE predictions, by voter type. In these plots, the AQRE predictions provide a much closer fit to our data than the PBE predictions, while also being consistent with the observed decrease in informedness as $c$ increases.²¹

Figure 5 illustrates observed decisions at each stage of the game when abstention is allowed, as well as the associated AQRE and PBE predictions. Note that the possibility of abstention means there are more potential errors to account for. In particular, informed voters can choose to abstain or to vote for the “incorrect” Option. Additionally, uninformed voters can choose not to abstain, thus incurring a cost of $\varepsilon$ =2. AQRE can account for each of these errors. It is especially noteworthy that this AQRE model explains the relatively high level of uninformed voting we observe and that such voting does not depend on voter type. Further, AQRE predictions regarding information acquisition fit our data well, especially for extreme types.

We next discuss our primary effect of interest: holding $c$ constant, how does varying the voting scheme affect behavior? This is particularly of interest since we chose to run the sessions with $c=15$ after observing data with $c=3$ and $c=9$ . Upon collecting this initial data, we found that AQRE provides a better explanation of behavior than PBE. We then noted that an AQRE (with $\lambda$ ‘s estimated from the initial data) predicted that informedness would be higher under abstention when $c=15$ . Thus, the second wave of data collection involves a test of an ex-ante hypothesis, which was formulated on the basis of an updated theory. Figure 6 illustrates observed behavior as well as the corresponding AQRE and PBE predictions. Note that the AQRE predictions are consistent with the observed behavior on the tails of the distribution of voter types. Further, notice that the AQRE predicts that allowing abstention will increase informedness when $c=15$ , which is consistent with our findings as discussed in section 4.1. For lower levels of $c$ , AQRE is consistent with our observation that informedness is higher when voting is mandatory.

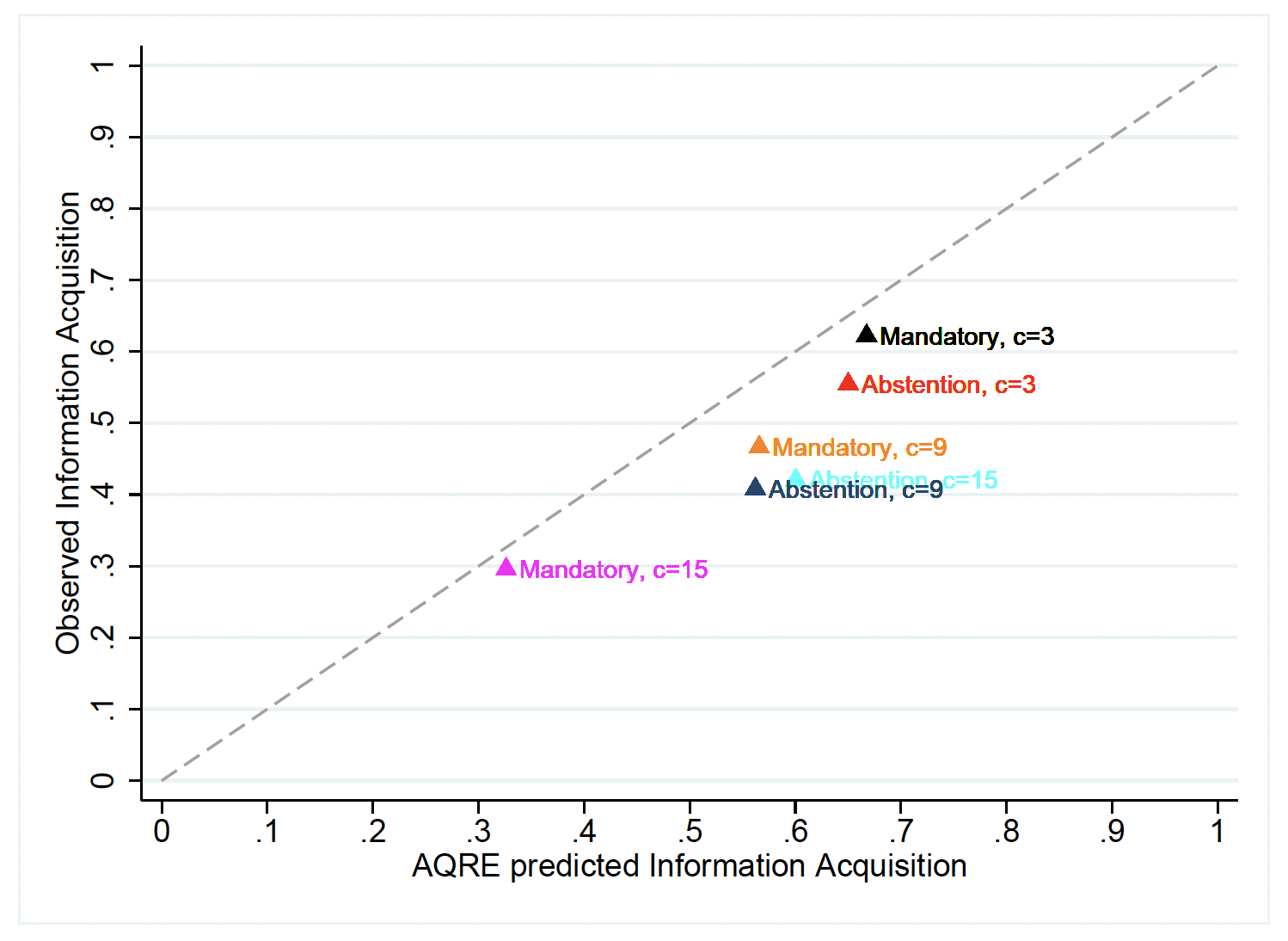
Overall, the AQRE model provides a much better fit for our data than the PBE predictions. This is further illustrated in Figure 7, which plots observed informedness by treatment against the AQRE predictions. Not only is AQRE able to account for the observed uninformed voting when abstention is possible, it accounts for the observed patterns of information acquisition.²²

5 Conclusion

This paper investigates how mandatory voting laws affect information acquisition in nonpartisan elections. In our model, voters have single-peaked preferences over policy outcomes, which are independent draws from a common-knowledge distribution (types are private information). There are two candidates in the election, each associated with different expected policy outcomes. The outcome associated with one candidate is on the left half of the support of voter types, while the other candidate is associated with the right half of this support. Candidates are indistinguishable to voters; each voter may learn candidate identities by incurring a private cost. After the information acquisition stage, costly voting takes place. We consider voting environments with and without abstention.

Our model predicts that mandatory voting laws will increase citizen informedness when information is cheap relative to the cost of voting and decrease citizen informedness when information is relatively expensive. The primary theoretical mechanism that predicts higher informedness when abstention is allowed is the increased probability of being the pivotal voter, since in equilibrium uninformed voters abstain when permitted to do so.

To evaluate these predictions we conducted a laboratory experiment. We varied whether or not abstention was permitted on a between-subject basis and the cost of information on a within-subject basis. We initially ran experiments for only two costs of information and found that when the cost was low, that informedness was higher when voting was mandatory. However, when the cost of information was increased, we found that uninformed subjects often voted when not required to do so. This reduced the value of information under abstention, since the probability of being the pivotal voter is reduced. As a result, informedness was not significantly different across voting schemes.

These results are well explained using agent quantal response equilibrium, which accounts for the observed errors that voters make in these games. Most importantly, AQRE predicts (in line with our initial data) that uninformed voters will sometimes vote, even when abstention is permitted. AQRE also predicts that a further increase in the cost of information would result in a higher level of informedness under abstention. To assess whether our preferred model has predictive power, we ran a second set of experiments to test this hypothesis. These experiments were identical to the first series, except that we evaluated a higher cost of information. The results are in line with the AQRE predictions, which increases our confidence in our conclusion that AQRE is an appropriate prediction tool in voting games such as ours.²³

Nonpartisan elections play a key role in determining public policy, especially at a local level. Often voters are unable to distinguish between candidates and there is no partisan cue to guide their decision. This leads to reduced election participation, which may reduce the effective accountability of these officials to voters. As such, finding ways to increase the informedness of voters in these elections is an important issue. Our results suggest that making voting mandatory in such elections may be an effective mechanism to increase informedness, even when the cost of becoming informed is relatively high, since the effect of increasing the cost of information is not as stark as predicted. Indeed, the cost of information needs to be quite high before making voting mandatory would reduce the level of informedness.

Variation in observed voting schemes is relatively rare. Thus, experimental and theoretical advances can help guide policy experiments to study the effects of mandatory voting in real-world environments. This paper is a first step in this direction. Moving forward, a particularly fruitful avenue for future research would be experiments studying the effect of differences in the cost of voting itself, or allowing candidates to endogenously select platforms in an environment in which these platforms are only observed at a cost. Future work could build on this model by accounting for voter preferences for candidate quality, in addition to partisanship.

6 Tables and Figures

Table 1: PBE Predictions

Under PBE, informed types always vote for their preferred candidate. When abstention is possible, only informed types vote. $[v_l^*,v_r^*]$ is the interval of types predicted by PBE to purchase information. PBE predictions for informedness are empirically weighted based on types realized in the experiment.

Table 2: Information Acquisition – Predicted and Observed

Means by treatment, with standard deviations in parentheses. PBE predictions are empirically weighted based on types realized in the experiment. Observed data are collapsed at the block level.

Table 3: Summary Statistics of Observed Behavior at the Voting Stage

$VC$ indicates a vote for the “correct” Option, and $VW$ a vote for the “wrong” Option. $abs$ indicates a voter chose to abstain. $e_i$ is an indicator variable that is equal to one if a subject paid to acquire information.

Figure 1: Voting game sequence.

At the voting stage, players can vote between the two candidates under mandatory voting, and have the additional option to abstain under the abstention treatment.

Figure 2: Predicted information acquisition

Information acquisition predictions for the parameterized experiment. $v\sim U[0,1]$ , $a\sim U[0,.5]$ and $b\sim U[.5,1]$ , with $\varepsilon=2$ and $n=5$ .

Figure 3: Predicted and actual information acquisition.

Data are averaged in blocks of ten by voter type. PBE cutpoint predictions are indicated by plus signs, where voter types outside the interval formed by the cutpoints are predicted to take the action indicated with probability one, and those inside the interval with probability zero.

Figure 4: All Decisions – Mandatory

Data are averaged in blocks of ten by voter type. PBE cutpoint predictions are indicated by plus signs, where voter types outside the interval formed by the cutpoints are predicted to take the action indicated with probability one, and those inside the interval with probability zero. AQRE predictions are displayed as dotted lines. $VW$ indicates a vote for the “wrong” Option.

Figure 5: All Decisions – Abstention

Data are averaged in blocks of ten by voter type. PBE cutpoint predictions are indicated by plus signs, where voter types outside the interval formed by the cutpoints are predicted to take the action indicated with probability one, and those inside the interval with probability zero. AQRE predictions are displayed as dotted lines. $VW$ indicates a vote for the “wrong” Option.

Figure 6: Information Acquisition with and without Abstention

Data are averaged in blocks of ten by voter type. PBE cutpoint predictions are indicated by plus signs, where voter types outside the interval formed by the cutpoints are predicted to take the action indicated with probability one, and those inside the interval with probability zero. AQRE predictions are displayed as dotted lines.

Figure 7: Information Acquisition – Predicted and Observed

Average information acquisition for each treatment, against AQRE predictions.

References

Bassi, A. (2015). Voting systems and strategic manipulation: An experimental study. Journal of Theoretical Politics 27 (1), 58–85.

Battaglini, M., R. B. Morton, and T. R. Palfrey (2008, May). Information aggregation and strategic abstention in large laboratory elections. American Economic Review 98 (2), 194–200.

Bhattacharya, S., J. Duffy, and S. Kim (2017). Voting with endogenous information acquisition: Experimental evidence. Games and Economic Behavior 102, 316–338.

Bonneau, C. and D. Cann (2015). Party identification and vote choice in partisan and nonpartisan elections. Political Behavior 37 (1), 43–66.

Börgers, T. (2004). Costly voting. American Economic Review 94 (1), 57–66.

Bowler, S., T. Donovan, and T. Happ (1992). Ballot propositions and information costs: Direct democracy and the fatigued voter. Western Political Quarterly 45 (2), 559–568.

Elbittar, A., A. Gomberg, C. Martinelli, and T. R. Palfrey (2020). Ignorance and bias in collective decisions. Journal of Economic Behavior & Organization 174, 332 – 359.

Feddersen, T. J. and W. Pesendorfer (1999). Abstention in elections with asymmetric information and diverse preferences. American Political Science Review 93 (2), 381–398.

Fischbacher, U. (2007). z-tree: Zurich toolbox for ready-made economic experiments. Experimental economics 10 (2), 171–178.

Gersbach, H. (1992). Allocation of information by majority decisions. Journal of Public Economics 48 (2), 259 – 268.

Ghirardato, P. and J. N. Katz (2006). Indecision theory: Weight of evidence and voting behavior. Journal of Public Economic Theory 8 (3), 379–399.

Ghosal, S. and B. Lockwood (2009, Jun). Costly voting when both information and preferences differ: is turnout too high or too low? Social Choice and Welfare 33 (1), 25–50.

Goeree, J. K. and C. A. Holt (2005). An explanation of anomalous behavior in models of political participation. American political science Review , 201–213.

Großer, J. and T. Palfrey (2014). Candidate entry and political polarization: An antimedian voter theorem. American Journal of Political Science 58 (1), 127–143.

Großer, J. and T. R. Palfrey (2019). Candidate entry and political polarization: An experimental study. American Political Science Review 113 (1), 209–225.

Großer, J. and M. Seebauer (2016). The curse of uninformed voting: An experimental study. Games and Economic Behavior 97, 205 – 226.

Hoffman, M., G. Léon, and M. Lombardi (2017). Compulsory voting, turnout, and government spending: Evidence from austria. Journal of Public Economics 145, 103 – 115.

Krasa, S. and M. K. Polborn (2009). Is mandatory voting better than voluntary voting? Games and Economic Behavior 66 (1), 275–291.

Krishna, V. and J. Morgan (2012). Voluntary voting: Costs and benefits. Journal of Economic Theory 147 (6), 2083 – 2123.

Lassen, D. D. (2005). The effect of information on voter turnout: Evidence from a natural experiment. American Journal of Political Science 49 (1), 103–118.

Levine, D. K. and T. R. Palfrey (2007). The paradox of voter participation? a laboratory study. American political science Review 101 (1), 143–158.

Lim, C. S. and J. M. Snyder Jr (2015). Is more information always better? party cues and candidate quality in us judicial elections. Journal of public Economics 128, 107–123.

Martinelli, C. (2006). Would rational voters acquire costly information? Journal of Economic Theory 129 (1), 225–251.

Martinelli, C. (2007). Rational ignorance and voting behavior. International Journal of Game Theory 35 (3), 315–335.

Matějka, F. and G. Tabellini (2017, September). Electoral competition with rationally inattentive voters.

McKelvey, R. and T. Palfrey (1995). Quantal response equilibria for normal form games. Games and economic behavior 10 (1), 6–38.

McKelvey, R. and T. Palfrey (1998). Quantal response equilibria for extensive form games. Experimental economics 1 (1), 9–41.

McKelvey, R. and J. Patty (2006). A theory of voting in large elections. Games and Economic Behavior 57 (1), 155–180.

Morton, R. B., M. Piovesan, and J.-R. Tyran (2019). The dark side of the vote: Biased voters, social information, and information aggregation through majority voting. Games and Economic Behavior 113, 461–481.

Oliveros, S. (2013). Abstention, ideology and information acquisition. Journal of Economic Theory 148 (3), 871 – 902.

Ortoleva, P. and E. Snowberg (2015, February). Overconfidence in political behavior. American Economic Review 105 (2), 504–35.

Rahn, W. (1993). The role of partisan stereotypes in information processing about political candidates. American Journal of Political Science 37, 472–496.

Roth, A. E. (1994). Lets keep the con out of experimental a methodological note. Empirical Economics 19 (2), 279–289.

Schaffner, B. and M. Streb (2002). The partisan heuristic in low-information elections. Public Opinion Quarterly 66 (4), 559–581.

Schaffner, B., M. Streb, and G. Wright (2001). Tearns without uniforms: The nonpartisan ballot in state and local elections. Political Research Quarterly 54 (1), 7–30.

Strömberg, D. (2004). Radio’s impact on public spending. The Quarterly Journal of Economics 119 (1), 189–221.

Tyszler, M. and A. Schram (2016). Information and strategic voting. Experimental economics 19 (2), 360–381.

Woods, D. (2023). Improving ex-ante power analysis with quantal response simulations. Working paper.

Does mandatory voting lead to more informed voting?

Executive Summary

Resources

Focuses

1 Introduction